Tijdschriftissue 2 2016

Wat heeft het nemen van beslissingen te maken met een ijsklontje?

• geschreven door Marieke M. J. W. van Rooij

Wat heeft het nemen van beslissingen te maken met een ijsklontje? Een vreemde vraag die toch relevant blijkt te zijn. Experimenten waarbij mensen werden gevraagd om verschillende keuzes te maken tussen een zekere en een risicovolle keuze hebben namelijk dezelfde soort patronen laten zien die natuurkundigen kennen van de overgang van ijs naar water. Dit leert ons op een andere manier te kijken naar het nemen van beslissingen.

 Afbeelding van Pixabay (https://pixabay.com/nl/ijsblokjes-koud-water-smelten-1224804/), CC0 (https://creativecommons.org/publicdomain/zero/1.0/deed.nl)

De vraag in de titel klinkt misschien als een absurde vraag, maar het is minder vreemd dan het op het eerste gezicht lijkt. Dit artikel gaat over een interessant experiment dat heeft laten zien dat de omslagpunten tussen risicozoekende en risicomijdende beslissingen erg lijken op de niet-lineaire overgang van ijs naar water (zie ook van Rooij, Favela, Malone, & Richardson, 2013). Sterker nog, het switchen tussen risicozoekende en risicomijdende beslissingen deelt eigenschappen met andere transities in de natuur. Psychologen zullen dus met andere ogen naar het nemen van beslissingen moeten gaan kijken en kunnen daarbij leren van de natuurwetenschappen.

Een belangrijke, maar vaak impliciete aanname binnen de cognitieve wetenschappen is lineariteit; het idee dat een kleine verandering in de omgeving of een taak ook een kleine verandering veroorzaakt in cognitief gedrag. Deze aanname ligt bijvoorbeeld ten grondslag aan reactietijd-experimenten. In dit soort experimenten krijgen proefpersonen twee soorten stimuli te verwerken. Verschillen in de gemiddelde tijd die het kost om op deze stimuli te reageren worden gezien als bewijs dat er ook een verschil is in de verwerking ervan. Dit wordt informatieverwerking genoemd (Sternberg, 1977).  Het idee is dat de mens bovenal een verwerker van informatie is, vergelijkbaar met een computer.

Echter, het idee dat menselijk gedrag lineair is en dat veranderingen in de input leiden tot even grote veranderingen in de reactie op deze input, wordt door steeds meer gedragswetenschappers betwist (bijv. Van Orden, Holden, & Turvey, 2003; 2005). Voor een alternatief kijkt men daarbij naar wetenschapsgebieden buiten de psychologie zoals wiskunde, natuurkunde en biologie.

Natuurwetenschappers weten namelijk al veel langer dat complexe systemen (zoals de mens) zich vaak helemaal niet lineair gedragen (bijv. Prigogine, 1984). Een voorbeeld daarvan is water, of in vaste vorm, ijs. Wat gebeurt er namelijk als je de omgevingstemperatuur van ijs laat stijgen van -10° naar -9° Celsius? Op het oog helemaal niks. Als je nu de omgevingstemperatuur van hetzelfde ijs laat stijgen van -1° naar 0° (een even grote verandering), verandert het van vast naar vloeibaar. Wat echter weinig mensen weten is dat als je de omgevingstemperatuur van water weer langzaam laat dalen, dat het dan bevriest bij een temperatuur van -4° in plaats van 0°. Alles bij elkaar wordt de toestand van water gekenmerkt door verschillende niet-lineaire fenomenen: Ten eerste veroorzaakt dezelfde verandering in de omgeving in sommige gevallen een veel dramatischere verandering dan in andere. Ten tweede is de toestand van water multistabiel; bij dezelfde temperatuur is water soms ijs, soms water. Ten derde, is er een grotere verandering in temperatuur nodig voor het weer bevriezen van water dan voor het smelten. 

Maar, wat heeft dit nu te maken met het nemen van beslissingen?

Het Experiment

In dit experiment worden proefpersonen gevraagd om 79 opeenvolgende keuzes te maken tussen een ‘een zeker verlies van $750’ en een risicovolle optie, bijv. ‘75% kans om $1500 te verliezen’., In dit specifieke voorbeeld kiest bijna iedereen voor de zekere optie. Bij de volgende keuze blijft de zekere optie hetzelfde, maar verandert de risicovolle optie met $25 naar ‘75% kans om $1475 te verliezen’. Elke volgende keuze wordt zo minder risicovol (het bedrag wordt steeds $25 minder) tot de risicovolle optie ‘75% kans om $750 te verliezen’ bedraagt (waarbij bijna iedereen deze optie kiest). Vervolgens worden de veranderingen weer ongedaan gemaakt: Het bedrag van de risicovolle optie gaat in stappen van $25 weer omhoog tot de oorspronkelijke optie ‘75% kans om $1500 te verliezen’ is bereikt. Op deze manier verwacht je dus tweemaal een omslagpunt, eenmaal van de keuze van de zekere optie naar de risicovolle optie en eenmaal andersom (beide rond ‘75% kans om $1000 te verliezen’, zie Figuur 1).

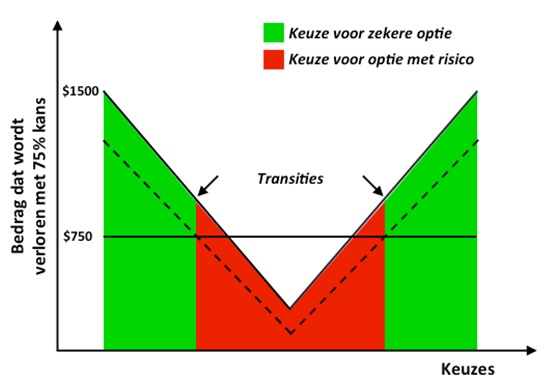Figuur 1. Het experiment bestaande uit 79 opeenvolgende keuzes waarbij het bedrag van de optie met het risico begint bij $1500, steeds kleiner wordt (tot het $750 bedraagt, en vervolgens weer steeds groter wordt. De stippellijn geeft het verwachte verlies van de optie met het risico weer (75% van het risico-bedrag). Als deze verwachting hoger is dan de zekere optie, (een verlies van $750), is de keuze voor de zekere optie optimaal. Als de verwachting lager is, is de keuze voor de optie met het risico optimaal. Op deze manier, veranderen proefpersonen dus twee keer van strategie.

 

Als je nu kijkt naar de keuzes van de proefpersonen zie je iets interessants. Bij meer dan de helft van de gevallen is de waarde van het bedrag behorend bij het tweede omslagpunt hoger dan bij het eerste omslagpunt.[1] Met andere woorden, op de terugweg, als de bedragen steeds weer een klein beetje terug veranderen, blijven proefpersonen langer kiezen voor de optie met het risico, dan op de heenweg. Dit is precies hetzelfde effect als we zien bij de transitie van ijs naar water en weer terug. Ook daar vindt het tweede omslagpunt later plaats dan wat je op basis van het eerste omslagpunt zou verwachten. In de natuurkunde wordt dit effect hysterese genoemd (voor het eerst aangetoond in magneten door Ewing, 1891). Hysterese is een belangrijk kenmerk van niet-lineaire veranderingen en blijkt dus ook voor te komen in complex cognitief gedrag zoals het nemen van beslissingen.

Een andere bevinding bij dit experiment was dat proefpersonen langer over hun keuze doen naarmate ze dichterbij een omslagpunt zijn en na het omslagpunt weer versnellen. Dit is wederom een bekend kenmerk van niet-lineaire transities en wordt critical slowing down genoemd. Dit fenomeen wordt veroorzaakt door het feit dat complexe systemen in de buurt van een omslagpunt instabieler zijn dan wanneer ze ver van een omslagpunt zijn. Door de instabiliteit van het cognitieve systeem dat ten grondslag ligt aan het nemen van beslissingen, duurt het langer voordat de keuze daadwerkelijk gemaakt wordt en vastligt.

Conclusie

De omslagpunten tussen risicozoekende en risicomijdende beslissingen lijken dus op de overgang van ijs naar water. Of tenminste, de veranderingen delen dezelfde soort niet-lineaire eigenschappen. Dit betekent dat ons inzicht in de manier waarop mensen beslissingen zou kunnen profiteren van wat natuurkundigen weten over niet-lineaire veranderingen. Dit vraagt om een andere manier van denken en experimenteren dan er binnen het huidige kader van informatieverwerking gebeurt. Psychologen kunnen daarbij veel leren van andere vakgebieden en zouden zich meer moeten focussen op niet-lineaire veranderingsprocessen.

Literatuurlijst

Ewing, J. A. (1881). Effects of Stress on the Thermoelectric Quality of Metals. Part I. Proceedings of the Royal Society of London (1854-1905) 32, 399–402.

Prigogine, I. (1984). Order out of chaos: Man's new dialogue with nature.

Sternberg, R. J. (1977). Intelligence, information processing, and analogical reasoning: The componential analysis of human abilities. Lawrence Erlbaum.

Van Orden, G. C., Holden, J. G., & Turvey, M. T. (2003). Self-organization of cognitive performance. Journal of Experimental Psychology: General, 132, 331-350.

Van Orden, G. C., Holden, J. G., & Turvey, M. T. (2005). Human cognition and 1/f scaling. Journal of Experimental Psychology: General, 134, 117-123.

van Rooij, M. M., Favela, L. H., Malone, M., & Richardson, M. J. (2013). Modeling the dynamics of risky choice. Ecological Psychology, 25, 293-303.